View Jupyter notebook on the GitHub.
Hierarchical time series#
This notebook contains examples of modelling hierarchical time series.
Table of contents
Hierarchical time series
Preparing dataset
Manually setting hierarchical structure
Hierarchical structure detection
Reconciliation methods
Bottom-up approach
Top-down approach
Exogenous variables for hierarchical forecasts
[1]:
import warnings
warnings.filterwarnings("ignore")
[2]:
import pandas as pd
from etna.metrics import SMAPE
from etna.models import LinearPerSegmentModel
from etna.pipeline import HierarchicalPipeline
from etna.pipeline import Pipeline
from etna.transforms import LagTransform
from etna.transforms import OneHotEncoderTransform
pd.options.display.max_columns = 100
1. Hierarchical time series#
In many applications time series have a natural level structure. Time series with such properties can be disaggregated by attributes from lower levels. On the other hand, this time series can be aggregated to higher levels to represent more general relations. The set of possible levels forms the hierarchy of time series.
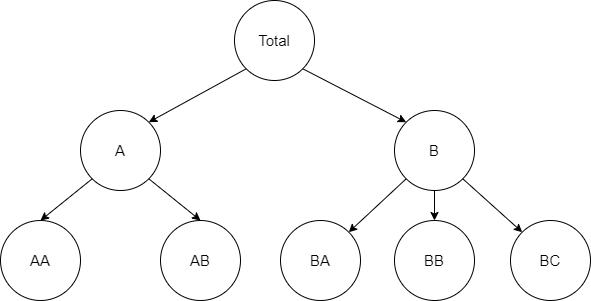
Two level hierarchical structure
Image above represents relations between members of the hierarchy. Middle and top levels can be disaggregated using members from lower levels. For example
In matrix notation level aggregation could be written as
where \(S\) - summing matrix.
2. Preparing dataset#
Consider the Australian tourism dataset.
This dataset consists of the following components:
Total- total domestic tourism demand,Tourism reasons components (
Holfor holiday,Busfor business, etc)Components representing the “region-reason” division (
NSW - hol,NSW - bus, etc)Components representing “region - reason - city” division (
NSW - hol - city,NSW - hol - noncity, etc)
We can see that these components form a hierarchy with the following levels:
Total
Tourism reason
Region
City
[3]:
!curl "https://robjhyndman.com/data/hier1_with_names.csv" --ssl-no-revoke -o "hier1_with_names.csv"
% Total % Received % Xferd Average Speed Time Time Time Current
Dload Upload Total Spent Left Speed
100 15664 100 15664 0 0 16533 0 --:--:-- --:--:-- --:--:-- 16646
[4]:
df = pd.read_csv("hier1_with_names.csv")
periods = len(df)
df["timestamp"] = pd.date_range("2006-01-01", periods=periods, freq="MS")
df.set_index("timestamp", inplace=True)
df.head()
[4]:
| Total | Hol | VFR | Bus | Oth | NSW - hol | VIC - hol | QLD - hol | SA - hol | WA - hol | TAS - hol | NT - hol | NSW - vfr | VIC - vfr | QLD - vfr | SA - vfr | WA - vfr | TAS - vfr | NT - vfr | NSW - bus | VIC - bus | QLD - bus | SA - bus | WA - bus | TAS - bus | NT - bus | NSW - oth | VIC - oth | QLD - oth | SA - oth | WA - oth | TAS - oth | NT - oth | NSW - hol - city | NSW - hol - noncity | VIC - hol - city | VIC - hol - noncity | QLD - hol - city | QLD - hol - noncity | SA - hol - city | SA - hol - noncity | WA - hol - city | WA - hol - noncity | TAS - hol - city | TAS - hol - noncity | NT - hol - city | NT - hol - noncity | NSW - vfr - city | NSW - vfr - noncity | VIC - vfr - city | VIC - vfr - noncity | QLD - vfr - city | QLD - vfr - noncity | SA - vfr - city | SA - vfr - noncity | WA - vfr - city | WA - vfr - noncity | TAS - vfr - city | TAS - vfr - noncity | NT - vfr - city | NT - vfr - noncity | NSW - bus - city | NSW - bus - noncity | VIC - bus - city | VIC - bus - noncity | QLD - bus - city | QLD - bus - noncity | SA - bus - city | SA - bus - noncity | WA - bus - city | WA - bus - noncity | TAS - bus - city | TAS - bus - noncity | NT - bus - city | NT - bus - noncity | NSW - oth - city | NSW - oth - noncity | VIC - oth - city | VIC - oth - noncity | QLD - oth - city | QLD - oth - noncity | SA - oth - city | SA - oth - noncity | WA - oth - city | WA - oth - noncity | TAS - oth - city | TAS - oth - noncity | NT - oth - city | NT - oth - noncity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| timestamp | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2006-01-01 | 84503 | 45906 | 26042 | 9815 | 2740 | 17589 | 10412 | 9078 | 3089 | 3449 | 2102 | 187 | 9398 | 5993 | 5290 | 2193 | 1781 | 1350 | 37 | 2885 | 2148 | 2093 | 844 | 1406 | 223 | 216 | 906 | 467 | 702 | 317 | 205 | 100 | 43 | 3096 | 14493 | 2531 | 7881 | 4688 | 4390 | 888 | 2201 | 1383 | 2066 | 619 | 1483 | 101 | 86 | 2709 | 6689 | 2565 | 3428 | 3003 | 2287 | 1324 | 869 | 1019 | 762 | 602 | 748 | 28 | 9 | 1201 | 1684 | 1164 | 984 | 1111 | 982 | 388 | 456 | 532 | 874 | 116 | 107 | 136 | 80 | 396 | 510 | 181 | 286 | 431 | 271 | 244 | 73 | 168 | 37 | 76 | 24 | 35 | 8 |
| 2006-02-01 | 65312 | 29347 | 20676 | 11823 | 3466 | 11027 | 6025 | 6310 | 1935 | 2454 | 1098 | 498 | 7829 | 4107 | 4902 | 1445 | 1353 | 523 | 517 | 4301 | 1825 | 2224 | 749 | 2043 | 373 | 308 | 1238 | 552 | 839 | 363 | 269 | 97 | 108 | 1479 | 9548 | 1439 | 4586 | 2320 | 3990 | 521 | 1414 | 1059 | 1395 | 409 | 689 | 201 | 297 | 2184 | 5645 | 1852 | 2255 | 1957 | 2945 | 806 | 639 | 750 | 603 | 257 | 266 | 168 | 349 | 2020 | 2281 | 1014 | 811 | 776 | 1448 | 346 | 403 | 356 | 1687 | 83 | 290 | 138 | 170 | 657 | 581 | 229 | 323 | 669 | 170 | 142 | 221 | 170 | 99 | 36 | 61 | 69 | 39 |
| 2006-03-01 | 72753 | 32492 | 20582 | 13565 | 6114 | 8910 | 5060 | 11733 | 1569 | 3398 | 458 | 1364 | 7277 | 3811 | 5489 | 1453 | 1687 | 391 | 474 | 4093 | 1944 | 3379 | 750 | 1560 | 303 | 1536 | 1433 | 446 | 1434 | 712 | 1546 | 55 | 488 | 1609 | 7301 | 1488 | 3572 | 4758 | 6975 | 476 | 1093 | 1101 | 2297 | 127 | 331 | 619 | 745 | 2225 | 5052 | 1882 | 1929 | 2619 | 2870 | 1078 | 375 | 953 | 734 | 130 | 261 | 390 | 84 | 1975 | 2118 | 1153 | 791 | 1079 | 2300 | 390 | 360 | 440 | 1120 | 196 | 107 | 452 | 1084 | 540 | 893 | 128 | 318 | 270 | 1164 | 397 | 315 | 380 | 1166 | 32 | 23 | 150 | 338 |
| 2006-04-01 | 70880 | 31813 | 21613 | 11478 | 5976 | 10658 | 5481 | 8109 | 2270 | 3561 | 1320 | 414 | 8303 | 5090 | 4441 | 1209 | 1714 | 394 | 462 | 3463 | 1753 | 2880 | 890 | 1791 | 298 | 403 | 1902 | 606 | 749 | 454 | 1549 | 91 | 625 | 1520 | 9138 | 1906 | 3575 | 3328 | 4781 | 571 | 1699 | 1128 | 2433 | 371 | 949 | 164 | 250 | 2918 | 5385 | 2208 | 2882 | 2097 | 2344 | 568 | 641 | 999 | 715 | 137 | 257 | 244 | 218 | 1500 | 1963 | 1245 | 508 | 1128 | 1752 | 255 | 635 | 539 | 1252 | 70 | 228 | 243 | 160 | 745 | 1157 | 270 | 336 | 214 | 535 | 194 | 260 | 410 | 1139 | 48 | 43 | 172 | 453 |
| 2006-05-01 | 86893 | 46793 | 26947 | 10027 | 3126 | 16152 | 10958 | 10047 | 3023 | 4287 | 2113 | 213 | 10386 | 6152 | 5636 | 1685 | 2026 | 784 | 278 | 3347 | 1522 | 2751 | 666 | 1023 | 335 | 383 | 984 | 558 | 1015 | 180 | 190 | 137 | 62 | 1958 | 14194 | 2517 | 8441 | 4930 | 5117 | 873 | 2150 | 1560 | 2727 | 523 | 1590 | 62 | 151 | 3154 | 7232 | 2988 | 3164 | 2703 | 2933 | 887 | 798 | 1396 | 630 | 347 | 437 | 153 | 125 | 1196 | 2151 | 950 | 572 | 1192 | 1559 | 386 | 280 | 582 | 441 | 130 | 205 | 194 | 189 | 426 | 558 | 265 | 293 | 458 | 557 | 147 | 33 | 162 | 28 | 77 | 60 | 15 | 47 |
2.1 Manually setting hierarchical structure#
This section presents how to set hierarchical structure and prepare data. We are going to create a hierarchical dataset with two levels: total demand and demand per tourism reason.
[5]:
from etna.datasets import TSDataset
Consider the Reason level of the hierarchy.
[6]:
reason_segments = ["Hol", "VFR", "Bus", "Oth"]
df[reason_segments].head()
[6]:
| Hol | VFR | Bus | Oth | |
|---|---|---|---|---|
| timestamp | ||||
| 2006-01-01 | 45906 | 26042 | 9815 | 2740 |
| 2006-02-01 | 29347 | 20676 | 11823 | 3466 |
| 2006-03-01 | 32492 | 20582 | 13565 | 6114 |
| 2006-04-01 | 31813 | 21613 | 11478 | 5976 |
| 2006-05-01 | 46793 | 26947 | 10027 | 3126 |
2.1.1 Convert dataset to ETNA wide format#
First, convert dataframe to ETNA long format.
[7]:
hierarchical_df = []
for segment_name in reason_segments:
segment = df[segment_name]
segment_slice = pd.DataFrame(
{"timestamp": segment.index, "target": segment.values, "segment": [segment_name] * periods}
)
hierarchical_df.append(segment_slice)
hierarchical_df = pd.concat(hierarchical_df, axis=0)
hierarchical_df.head()
[7]:
| timestamp | target | segment | |
|---|---|---|---|
| 0 | 2006-01-01 | 45906 | Hol |
| 1 | 2006-02-01 | 29347 | Hol |
| 2 | 2006-03-01 | 32492 | Hol |
| 3 | 2006-04-01 | 31813 | Hol |
| 4 | 2006-05-01 | 46793 | Hol |
Now, the dataframe could be converted to ETNA wide format.
[8]:
hierarchical_df = TSDataset.to_dataset(df=hierarchical_df)
2.1.2 Creat HierarchicalStructure#
For handling information about hierarchical structure, there is a dedicated object in the ETNA library: HierarchicalStructure.
To create HierarchicalStructure define relationships between segments at different levels. This relation should be described as mapping between levels members, where keys are parent segments and values are lists of child segments from the lower level. Also provide a list of level names, where ordering corresponds to hierarchical relationships between levels.
[9]:
from etna.datasets import HierarchicalStructure
[10]:
hierarchical_structure = HierarchicalStructure(
level_structure={"total": ["Hol", "VFR", "Bus", "Oth"]}, level_names=["total", "reason"]
)
hierarchical_structure
[10]:
HierarchicalStructure(level_structure = {'total': ['Hol', 'VFR', 'Bus', 'Oth']}, level_names = ['total', 'reason'], )
2.1.3 Create hierarchical dataset#
When all the data is prepared, call the TSDataset constructor to create a hierarchical dataset.
[11]:
hierarchical_ts = TSDataset(df=hierarchical_df, freq="MS", hierarchical_structure=hierarchical_structure)
hierarchical_ts.head()
[11]:
| segment | Bus | Hol | Oth | VFR |
|---|---|---|---|---|
| feature | target | target | target | target |
| timestamp | ||||
| 2006-01-01 | 9815 | 45906 | 2740 | 26042 |
| 2006-02-01 | 11823 | 29347 | 3466 | 20676 |
| 2006-03-01 | 13565 | 32492 | 6114 | 20582 |
| 2006-04-01 | 11478 | 31813 | 5976 | 21613 |
| 2006-05-01 | 10027 | 46793 | 3126 | 26947 |
Ensure that the dataset is at the desired level.
[12]:
hierarchical_ts.current_df_level
[12]:
'reason'
2.2 Hierarchical structure detection#
This section presents how to prepare data and detect hierarchical structure. The main advantage of this approach for creating hierarchical structures is that you don’t need to define an adjacency list. All hierarchical relationships would be detected from the dataframe columns.
The main applications for this approach are when defining the adjacency list is not desirable or when some columns of the dataframe already have information about hierarchy (e.g. related categorical columns).
A data frame must be prepared in a specific format for detection to work. The following sections show how to do so.
Consider the City level of the hierarchy.
[13]:
city_segments = list(filter(lambda name: name.count("-") == 2, df.columns))
df[city_segments].head()
[13]:
| NSW - hol - city | NSW - hol - noncity | VIC - hol - city | VIC - hol - noncity | QLD - hol - city | QLD - hol - noncity | SA - hol - city | SA - hol - noncity | WA - hol - city | WA - hol - noncity | TAS - hol - city | TAS - hol - noncity | NT - hol - city | NT - hol - noncity | NSW - vfr - city | NSW - vfr - noncity | VIC - vfr - city | VIC - vfr - noncity | QLD - vfr - city | QLD - vfr - noncity | SA - vfr - city | SA - vfr - noncity | WA - vfr - city | WA - vfr - noncity | TAS - vfr - city | TAS - vfr - noncity | NT - vfr - city | NT - vfr - noncity | NSW - bus - city | NSW - bus - noncity | VIC - bus - city | VIC - bus - noncity | QLD - bus - city | QLD - bus - noncity | SA - bus - city | SA - bus - noncity | WA - bus - city | WA - bus - noncity | TAS - bus - city | TAS - bus - noncity | NT - bus - city | NT - bus - noncity | NSW - oth - city | NSW - oth - noncity | VIC - oth - city | VIC - oth - noncity | QLD - oth - city | QLD - oth - noncity | SA - oth - city | SA - oth - noncity | WA - oth - city | WA - oth - noncity | TAS - oth - city | TAS - oth - noncity | NT - oth - city | NT - oth - noncity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| timestamp | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2006-01-01 | 3096 | 14493 | 2531 | 7881 | 4688 | 4390 | 888 | 2201 | 1383 | 2066 | 619 | 1483 | 101 | 86 | 2709 | 6689 | 2565 | 3428 | 3003 | 2287 | 1324 | 869 | 1019 | 762 | 602 | 748 | 28 | 9 | 1201 | 1684 | 1164 | 984 | 1111 | 982 | 388 | 456 | 532 | 874 | 116 | 107 | 136 | 80 | 396 | 510 | 181 | 286 | 431 | 271 | 244 | 73 | 168 | 37 | 76 | 24 | 35 | 8 |
| 2006-02-01 | 1479 | 9548 | 1439 | 4586 | 2320 | 3990 | 521 | 1414 | 1059 | 1395 | 409 | 689 | 201 | 297 | 2184 | 5645 | 1852 | 2255 | 1957 | 2945 | 806 | 639 | 750 | 603 | 257 | 266 | 168 | 349 | 2020 | 2281 | 1014 | 811 | 776 | 1448 | 346 | 403 | 356 | 1687 | 83 | 290 | 138 | 170 | 657 | 581 | 229 | 323 | 669 | 170 | 142 | 221 | 170 | 99 | 36 | 61 | 69 | 39 |
| 2006-03-01 | 1609 | 7301 | 1488 | 3572 | 4758 | 6975 | 476 | 1093 | 1101 | 2297 | 127 | 331 | 619 | 745 | 2225 | 5052 | 1882 | 1929 | 2619 | 2870 | 1078 | 375 | 953 | 734 | 130 | 261 | 390 | 84 | 1975 | 2118 | 1153 | 791 | 1079 | 2300 | 390 | 360 | 440 | 1120 | 196 | 107 | 452 | 1084 | 540 | 893 | 128 | 318 | 270 | 1164 | 397 | 315 | 380 | 1166 | 32 | 23 | 150 | 338 |
| 2006-04-01 | 1520 | 9138 | 1906 | 3575 | 3328 | 4781 | 571 | 1699 | 1128 | 2433 | 371 | 949 | 164 | 250 | 2918 | 5385 | 2208 | 2882 | 2097 | 2344 | 568 | 641 | 999 | 715 | 137 | 257 | 244 | 218 | 1500 | 1963 | 1245 | 508 | 1128 | 1752 | 255 | 635 | 539 | 1252 | 70 | 228 | 243 | 160 | 745 | 1157 | 270 | 336 | 214 | 535 | 194 | 260 | 410 | 1139 | 48 | 43 | 172 | 453 |
| 2006-05-01 | 1958 | 14194 | 2517 | 8441 | 4930 | 5117 | 873 | 2150 | 1560 | 2727 | 523 | 1590 | 62 | 151 | 3154 | 7232 | 2988 | 3164 | 2703 | 2933 | 887 | 798 | 1396 | 630 | 347 | 437 | 153 | 125 | 1196 | 2151 | 950 | 572 | 1192 | 1559 | 386 | 280 | 582 | 441 | 130 | 205 | 194 | 189 | 426 | 558 | 265 | 293 | 458 | 557 | 147 | 33 | 162 | 28 | 77 | 60 | 15 | 47 |
2.2.1 Prepare data in ETNA hierarchical long format#
Before trying to detect a hierarchical structure, data must be transformed to hierarchical long format. In this format, your DataFrame must contain timestamp, target and level columns. Each level column represents membership of the observation at higher levels of the hierarchy.
[14]:
hierarchical_df = []
for segment_name in city_segments:
segment = df[segment_name]
region, reason, city = segment_name.split(" - ")
seg_df = pd.DataFrame(
data={
"timestamp": segment.index,
"target": segment.values,
"city_level": [city] * periods,
"region_level": [region] * periods,
"reason_level": [reason] * periods,
},
)
hierarchical_df.append(seg_df)
hierarchical_df = pd.concat(hierarchical_df, axis=0)
hierarchical_df["reason_level"].replace({"hol": "Hol", "vfr": "VFR", "bus": "Bus", "oth": "Oth"}, inplace=True)
hierarchical_df.head()
[14]:
| timestamp | target | city_level | region_level | reason_level | |
|---|---|---|---|---|---|
| 0 | 2006-01-01 | 3096 | city | NSW | Hol |
| 1 | 2006-02-01 | 1479 | city | NSW | Hol |
| 2 | 2006-03-01 | 1609 | city | NSW | Hol |
| 3 | 2006-04-01 | 1520 | city | NSW | Hol |
| 4 | 2006-05-01 | 1958 | city | NSW | Hol |
Here we can omit total level as it will be added automatically in hierarchy detection.
2.2.2 Convert data to etna wide format with to_hierarchical_dataset#
To detect hierarchical structure and convert DataFrame to ETNA wide format, call TSDataset.to_hierarchical_dataset, provided with prepared data and level columns names in order from top to bottom.
[15]:
hierarchical_df, hierarchical_structure = TSDataset.to_hierarchical_dataset(
df=hierarchical_df, level_columns=["reason_level", "region_level", "city_level"]
)
hierarchical_df.head()
[15]:
| segment | Bus_NSW_city | Bus_NSW_noncity | Bus_NT_city | Bus_NT_noncity | Bus_QLD_city | Bus_QLD_noncity | Bus_SA_city | Bus_SA_noncity | Bus_TAS_city | Bus_TAS_noncity | Bus_VIC_city | Bus_VIC_noncity | Bus_WA_city | Bus_WA_noncity | Hol_NSW_city | Hol_NSW_noncity | Hol_NT_city | Hol_NT_noncity | Hol_QLD_city | Hol_QLD_noncity | Hol_SA_city | Hol_SA_noncity | Hol_TAS_city | Hol_TAS_noncity | Hol_VIC_city | Hol_VIC_noncity | Hol_WA_city | Hol_WA_noncity | Oth_NSW_city | Oth_NSW_noncity | Oth_NT_city | Oth_NT_noncity | Oth_QLD_city | Oth_QLD_noncity | Oth_SA_city | Oth_SA_noncity | Oth_TAS_city | Oth_TAS_noncity | Oth_VIC_city | Oth_VIC_noncity | Oth_WA_city | Oth_WA_noncity | VFR_NSW_city | VFR_NSW_noncity | VFR_NT_city | VFR_NT_noncity | VFR_QLD_city | VFR_QLD_noncity | VFR_SA_city | VFR_SA_noncity | VFR_TAS_city | VFR_TAS_noncity | VFR_VIC_city | VFR_VIC_noncity | VFR_WA_city | VFR_WA_noncity |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| feature | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target |
| timestamp | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2006-01-01 | 1201 | 1684 | 136 | 80 | 1111 | 982 | 388 | 456 | 116 | 107 | 1164 | 984 | 532 | 874 | 3096 | 14493 | 101 | 86 | 4688 | 4390 | 888 | 2201 | 619 | 1483 | 2531 | 7881 | 1383 | 2066 | 396 | 510 | 35 | 8 | 431 | 271 | 244 | 73 | 76 | 24 | 181 | 286 | 168 | 37 | 2709 | 6689 | 28 | 9 | 3003 | 2287 | 1324 | 869 | 602 | 748 | 2565 | 3428 | 1019 | 762 |
| 2006-02-01 | 2020 | 2281 | 138 | 170 | 776 | 1448 | 346 | 403 | 83 | 290 | 1014 | 811 | 356 | 1687 | 1479 | 9548 | 201 | 297 | 2320 | 3990 | 521 | 1414 | 409 | 689 | 1439 | 4586 | 1059 | 1395 | 657 | 581 | 69 | 39 | 669 | 170 | 142 | 221 | 36 | 61 | 229 | 323 | 170 | 99 | 2184 | 5645 | 168 | 349 | 1957 | 2945 | 806 | 639 | 257 | 266 | 1852 | 2255 | 750 | 603 |
| 2006-03-01 | 1975 | 2118 | 452 | 1084 | 1079 | 2300 | 390 | 360 | 196 | 107 | 1153 | 791 | 440 | 1120 | 1609 | 7301 | 619 | 745 | 4758 | 6975 | 476 | 1093 | 127 | 331 | 1488 | 3572 | 1101 | 2297 | 540 | 893 | 150 | 338 | 270 | 1164 | 397 | 315 | 32 | 23 | 128 | 318 | 380 | 1166 | 2225 | 5052 | 390 | 84 | 2619 | 2870 | 1078 | 375 | 130 | 261 | 1882 | 1929 | 953 | 734 |
| 2006-04-01 | 1500 | 1963 | 243 | 160 | 1128 | 1752 | 255 | 635 | 70 | 228 | 1245 | 508 | 539 | 1252 | 1520 | 9138 | 164 | 250 | 3328 | 4781 | 571 | 1699 | 371 | 949 | 1906 | 3575 | 1128 | 2433 | 745 | 1157 | 172 | 453 | 214 | 535 | 194 | 260 | 48 | 43 | 270 | 336 | 410 | 1139 | 2918 | 5385 | 244 | 218 | 2097 | 2344 | 568 | 641 | 137 | 257 | 2208 | 2882 | 999 | 715 |
| 2006-05-01 | 1196 | 2151 | 194 | 189 | 1192 | 1559 | 386 | 280 | 130 | 205 | 950 | 572 | 582 | 441 | 1958 | 14194 | 62 | 151 | 4930 | 5117 | 873 | 2150 | 523 | 1590 | 2517 | 8441 | 1560 | 2727 | 426 | 558 | 15 | 47 | 458 | 557 | 147 | 33 | 77 | 60 | 265 | 293 | 162 | 28 | 3154 | 7232 | 153 | 125 | 2703 | 2933 | 887 | 798 | 347 | 437 | 2988 | 3164 | 1396 | 630 |
[16]:
hierarchical_structure
[16]:
HierarchicalStructure(level_structure = {'total': ['Hol', 'VFR', 'Bus', 'Oth'], 'Bus': ['Bus_NSW', 'Bus_VIC', 'Bus_QLD', 'Bus_SA', 'Bus_WA', 'Bus_TAS', 'Bus_NT'], 'Hol': ['Hol_NSW', 'Hol_VIC', 'Hol_QLD', 'Hol_SA', 'Hol_WA', 'Hol_TAS', 'Hol_NT'], 'Oth': ['Oth_NSW', 'Oth_VIC', 'Oth_QLD', 'Oth_SA', 'Oth_WA', 'Oth_TAS', 'Oth_NT'], 'VFR': ['VFR_NSW', 'VFR_VIC', 'VFR_QLD', 'VFR_SA', 'VFR_WA', 'VFR_TAS', 'VFR_NT'], 'Bus_NSW': ['Bus_NSW_city', 'Bus_NSW_noncity'], 'Bus_NT': ['Bus_NT_city', 'Bus_NT_noncity'], 'Bus_QLD': ['Bus_QLD_city', 'Bus_QLD_noncity'], 'Bus_SA': ['Bus_SA_city', 'Bus_SA_noncity'], 'Bus_TAS': ['Bus_TAS_city', 'Bus_TAS_noncity'], 'Bus_VIC': ['Bus_VIC_city', 'Bus_VIC_noncity'], 'Bus_WA': ['Bus_WA_city', 'Bus_WA_noncity'], 'Hol_NSW': ['Hol_NSW_city', 'Hol_NSW_noncity'], 'Hol_NT': ['Hol_NT_city', 'Hol_NT_noncity'], 'Hol_QLD': ['Hol_QLD_city', 'Hol_QLD_noncity'], 'Hol_SA': ['Hol_SA_city', 'Hol_SA_noncity'], 'Hol_TAS': ['Hol_TAS_city', 'Hol_TAS_noncity'], 'Hol_VIC': ['Hol_VIC_city', 'Hol_VIC_noncity'], 'Hol_WA': ['Hol_WA_city', 'Hol_WA_noncity'], 'Oth_NSW': ['Oth_NSW_city', 'Oth_NSW_noncity'], 'Oth_NT': ['Oth_NT_city', 'Oth_NT_noncity'], 'Oth_QLD': ['Oth_QLD_city', 'Oth_QLD_noncity'], 'Oth_SA': ['Oth_SA_city', 'Oth_SA_noncity'], 'Oth_TAS': ['Oth_TAS_city', 'Oth_TAS_noncity'], 'Oth_VIC': ['Oth_VIC_city', 'Oth_VIC_noncity'], 'Oth_WA': ['Oth_WA_city', 'Oth_WA_noncity'], 'VFR_NSW': ['VFR_NSW_city', 'VFR_NSW_noncity'], 'VFR_NT': ['VFR_NT_city', 'VFR_NT_noncity'], 'VFR_QLD': ['VFR_QLD_city', 'VFR_QLD_noncity'], 'VFR_SA': ['VFR_SA_city', 'VFR_SA_noncity'], 'VFR_TAS': ['VFR_TAS_city', 'VFR_TAS_noncity'], 'VFR_VIC': ['VFR_VIC_city', 'VFR_VIC_noncity'], 'VFR_WA': ['VFR_WA_city', 'VFR_WA_noncity']}, level_names = ['total', 'reason_level', 'region_level', 'city_level'], )
Here we see that hierarchical_structure has a mapping between higher level segments and adjacent lower level segments.
2.2.3 Create the hierarchical dataset#
To convert data to TSDataset call the constructor and pass detected hierarchical_structure.
[17]:
hierarchical_ts = TSDataset(df=hierarchical_df, freq="MS", hierarchical_structure=hierarchical_structure)
hierarchical_ts.head()
[17]:
| segment | Bus_NSW_city | Bus_NSW_noncity | Bus_NT_city | Bus_NT_noncity | Bus_QLD_city | Bus_QLD_noncity | Bus_SA_city | Bus_SA_noncity | Bus_TAS_city | Bus_TAS_noncity | Bus_VIC_city | Bus_VIC_noncity | Bus_WA_city | Bus_WA_noncity | Hol_NSW_city | Hol_NSW_noncity | Hol_NT_city | Hol_NT_noncity | Hol_QLD_city | Hol_QLD_noncity | Hol_SA_city | Hol_SA_noncity | Hol_TAS_city | Hol_TAS_noncity | Hol_VIC_city | Hol_VIC_noncity | Hol_WA_city | Hol_WA_noncity | Oth_NSW_city | Oth_NSW_noncity | Oth_NT_city | Oth_NT_noncity | Oth_QLD_city | Oth_QLD_noncity | Oth_SA_city | Oth_SA_noncity | Oth_TAS_city | Oth_TAS_noncity | Oth_VIC_city | Oth_VIC_noncity | Oth_WA_city | Oth_WA_noncity | VFR_NSW_city | VFR_NSW_noncity | VFR_NT_city | VFR_NT_noncity | VFR_QLD_city | VFR_QLD_noncity | VFR_SA_city | VFR_SA_noncity | VFR_TAS_city | VFR_TAS_noncity | VFR_VIC_city | VFR_VIC_noncity | VFR_WA_city | VFR_WA_noncity |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| feature | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target |
| timestamp | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2006-01-01 | 1201 | 1684 | 136 | 80 | 1111 | 982 | 388 | 456 | 116 | 107 | 1164 | 984 | 532 | 874 | 3096 | 14493 | 101 | 86 | 4688 | 4390 | 888 | 2201 | 619 | 1483 | 2531 | 7881 | 1383 | 2066 | 396 | 510 | 35 | 8 | 431 | 271 | 244 | 73 | 76 | 24 | 181 | 286 | 168 | 37 | 2709 | 6689 | 28 | 9 | 3003 | 2287 | 1324 | 869 | 602 | 748 | 2565 | 3428 | 1019 | 762 |
| 2006-02-01 | 2020 | 2281 | 138 | 170 | 776 | 1448 | 346 | 403 | 83 | 290 | 1014 | 811 | 356 | 1687 | 1479 | 9548 | 201 | 297 | 2320 | 3990 | 521 | 1414 | 409 | 689 | 1439 | 4586 | 1059 | 1395 | 657 | 581 | 69 | 39 | 669 | 170 | 142 | 221 | 36 | 61 | 229 | 323 | 170 | 99 | 2184 | 5645 | 168 | 349 | 1957 | 2945 | 806 | 639 | 257 | 266 | 1852 | 2255 | 750 | 603 |
| 2006-03-01 | 1975 | 2118 | 452 | 1084 | 1079 | 2300 | 390 | 360 | 196 | 107 | 1153 | 791 | 440 | 1120 | 1609 | 7301 | 619 | 745 | 4758 | 6975 | 476 | 1093 | 127 | 331 | 1488 | 3572 | 1101 | 2297 | 540 | 893 | 150 | 338 | 270 | 1164 | 397 | 315 | 32 | 23 | 128 | 318 | 380 | 1166 | 2225 | 5052 | 390 | 84 | 2619 | 2870 | 1078 | 375 | 130 | 261 | 1882 | 1929 | 953 | 734 |
| 2006-04-01 | 1500 | 1963 | 243 | 160 | 1128 | 1752 | 255 | 635 | 70 | 228 | 1245 | 508 | 539 | 1252 | 1520 | 9138 | 164 | 250 | 3328 | 4781 | 571 | 1699 | 371 | 949 | 1906 | 3575 | 1128 | 2433 | 745 | 1157 | 172 | 453 | 214 | 535 | 194 | 260 | 48 | 43 | 270 | 336 | 410 | 1139 | 2918 | 5385 | 244 | 218 | 2097 | 2344 | 568 | 641 | 137 | 257 | 2208 | 2882 | 999 | 715 |
| 2006-05-01 | 1196 | 2151 | 194 | 189 | 1192 | 1559 | 386 | 280 | 130 | 205 | 950 | 572 | 582 | 441 | 1958 | 14194 | 62 | 151 | 4930 | 5117 | 873 | 2150 | 523 | 1590 | 2517 | 8441 | 1560 | 2727 | 426 | 558 | 15 | 47 | 458 | 557 | 147 | 33 | 77 | 60 | 265 | 293 | 162 | 28 | 3154 | 7232 | 153 | 125 | 2703 | 2933 | 887 | 798 | 347 | 437 | 2988 | 3164 | 1396 | 630 |
Now the dataset converted to hierarchical. We can examine what hierarchical levels were detected with the following code.
[18]:
hierarchical_ts.hierarchical_structure.level_names
[18]:
['total', 'reason_level', 'region_level', 'city_level']
Ensure that the dataset is at the desired level.
[19]:
hierarchical_ts.current_df_level
[19]:
'city_level'
The hierarchical dataset could be aggregated to higher levels with the get_level_dataset method.
[20]:
hierarchical_ts.get_level_dataset(target_level="reason_level").head()
[20]:
| segment | Bus | Hol | Oth | VFR |
|---|---|---|---|---|
| feature | target | target | target | target |
| timestamp | ||||
| 2006-01-01 | 9815 | 45906 | 2740 | 26042 |
| 2006-02-01 | 11823 | 29347 | 3466 | 20676 |
| 2006-03-01 | 13565 | 32492 | 6114 | 20582 |
| 2006-04-01 | 11478 | 31813 | 5976 | 21613 |
| 2006-05-01 | 10027 | 46793 | 3126 | 26947 |
3. Reconciliation methods#
In this section we will examine the reconciliation methods available in ETNA. Hierarchical time series reconciliation allows for the readjustment of predictions produced by separate models on a set of hierarchically linked time series in order to make the forecasts more accurate, and ensure that they are coherent.
There are several reconciliation methods in the ETNA library:
Bottom-up approach
Top-down approach
Middle-out reconciliation approach could be viewed as a composition of bottom-up and top-down approaches. This method could be implemented using functionality from the library. For aggregation to higher levels, one could use provided bottom-up methods, and for disaggregation to lower levels – top-down methods.
Reconciliation methods estimate mapping matrices to perform transitions between levels. These matrices are sparse. ETNA uses scipy.sparse.csr_matrix to efficiently store them and perform computation.
More detailed information about this and other reconciliation methods can be found here.
Some important definitions:
source level - level of the hierarchy for model estimation, reconciliation applied to this level
target level - desired level of the hierarchy, after reconciliation we want to have series at this level.
3.1. Bottom-up approach#
The main idea of this approach is to produce forecasts for time series at lower hierarchical levels and then perform aggregation to higher levels.
where \(h\) - forecast horizon.
In matrix notation:
An advantage of this approach is that we are forecasting at the bottom-level of a structure and are able to capture all the patterns of the individual series. On the other hand, bottom-level data can be quite noisy and more challenging to model and forecast.
[21]:
from etna.reconciliation import BottomUpReconciliator
To create BottomUpReconciliator specify “source” and “target” levels for aggregation. Make sure that the source level is lower in the hierarchy than the target level.
[22]:
reconciliator = BottomUpReconciliator(target_level="region_level", source_level="city_level")
The next step is mapping matrix estimation. To do so pass hierarchical dataset to fit method. Current dataset level should be lower or equal to source level.
[23]:
reconciliator.fit(ts=hierarchical_ts)
reconciliator.mapping_matrix.toarray()
[23]:
array([[1, 1, 0, ..., 0, 0, 0],
[0, 0, 1, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
...,
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 1, 0, 0],
[0, 0, 0, ..., 0, 1, 1]], dtype=int32)
Now reconciliator is ready to perform aggregation to target level.
[24]:
reconciliator.aggregate(ts=hierarchical_ts).head(5)
[24]:
| segment | Bus_NSW_city | Bus_NSW_noncity | Bus_NT_city | Bus_NT_noncity | Bus_QLD_city | Bus_QLD_noncity | Bus_SA_city | Bus_SA_noncity | Bus_TAS_city | Bus_TAS_noncity | Bus_VIC_city | Bus_VIC_noncity | Bus_WA_city | Bus_WA_noncity | Hol_NSW_city | Hol_NSW_noncity | Hol_NT_city | Hol_NT_noncity | Hol_QLD_city | Hol_QLD_noncity | Hol_SA_city | Hol_SA_noncity | Hol_TAS_city | Hol_TAS_noncity | Hol_VIC_city | Hol_VIC_noncity | Hol_WA_city | Hol_WA_noncity | Oth_NSW_city | Oth_NSW_noncity | Oth_NT_city | Oth_NT_noncity | Oth_QLD_city | Oth_QLD_noncity | Oth_SA_city | Oth_SA_noncity | Oth_TAS_city | Oth_TAS_noncity | Oth_VIC_city | Oth_VIC_noncity | Oth_WA_city | Oth_WA_noncity | VFR_NSW_city | VFR_NSW_noncity | VFR_NT_city | VFR_NT_noncity | VFR_QLD_city | VFR_QLD_noncity | VFR_SA_city | VFR_SA_noncity | VFR_TAS_city | VFR_TAS_noncity | VFR_VIC_city | VFR_VIC_noncity | VFR_WA_city | VFR_WA_noncity |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| feature | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target |
| timestamp | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2006-01-01 | 1201 | 1684 | 136 | 80 | 1111 | 982 | 388 | 456 | 116 | 107 | 1164 | 984 | 532 | 874 | 3096 | 14493 | 101 | 86 | 4688 | 4390 | 888 | 2201 | 619 | 1483 | 2531 | 7881 | 1383 | 2066 | 396 | 510 | 35 | 8 | 431 | 271 | 244 | 73 | 76 | 24 | 181 | 286 | 168 | 37 | 2709 | 6689 | 28 | 9 | 3003 | 2287 | 1324 | 869 | 602 | 748 | 2565 | 3428 | 1019 | 762 |
| 2006-02-01 | 2020 | 2281 | 138 | 170 | 776 | 1448 | 346 | 403 | 83 | 290 | 1014 | 811 | 356 | 1687 | 1479 | 9548 | 201 | 297 | 2320 | 3990 | 521 | 1414 | 409 | 689 | 1439 | 4586 | 1059 | 1395 | 657 | 581 | 69 | 39 | 669 | 170 | 142 | 221 | 36 | 61 | 229 | 323 | 170 | 99 | 2184 | 5645 | 168 | 349 | 1957 | 2945 | 806 | 639 | 257 | 266 | 1852 | 2255 | 750 | 603 |
| 2006-03-01 | 1975 | 2118 | 452 | 1084 | 1079 | 2300 | 390 | 360 | 196 | 107 | 1153 | 791 | 440 | 1120 | 1609 | 7301 | 619 | 745 | 4758 | 6975 | 476 | 1093 | 127 | 331 | 1488 | 3572 | 1101 | 2297 | 540 | 893 | 150 | 338 | 270 | 1164 | 397 | 315 | 32 | 23 | 128 | 318 | 380 | 1166 | 2225 | 5052 | 390 | 84 | 2619 | 2870 | 1078 | 375 | 130 | 261 | 1882 | 1929 | 953 | 734 |
| 2006-04-01 | 1500 | 1963 | 243 | 160 | 1128 | 1752 | 255 | 635 | 70 | 228 | 1245 | 508 | 539 | 1252 | 1520 | 9138 | 164 | 250 | 3328 | 4781 | 571 | 1699 | 371 | 949 | 1906 | 3575 | 1128 | 2433 | 745 | 1157 | 172 | 453 | 214 | 535 | 194 | 260 | 48 | 43 | 270 | 336 | 410 | 1139 | 2918 | 5385 | 244 | 218 | 2097 | 2344 | 568 | 641 | 137 | 257 | 2208 | 2882 | 999 | 715 |
| 2006-05-01 | 1196 | 2151 | 194 | 189 | 1192 | 1559 | 386 | 280 | 130 | 205 | 950 | 572 | 582 | 441 | 1958 | 14194 | 62 | 151 | 4930 | 5117 | 873 | 2150 | 523 | 1590 | 2517 | 8441 | 1560 | 2727 | 426 | 558 | 15 | 47 | 458 | 557 | 147 | 33 | 77 | 60 | 265 | 293 | 162 | 28 | 3154 | 7232 | 153 | 125 | 2703 | 2933 | 887 | 798 | 347 | 437 | 2988 | 3164 | 1396 | 630 |
HierarchicalPipeline provides the ability to perform forecasts reconciliation in pipeline. A couple of points to keep in mind while working with this type of pipeline:
Transforms and model work with the dataset on the source level.
Forecasts are automatically reconciliated to the target level, metrics reported for target level as well.
[25]:
pipeline = HierarchicalPipeline(
transforms=[
LagTransform(in_column="target", lags=[1, 2, 3, 4, 6, 12]),
],
model=LinearPerSegmentModel(),
reconciliator=BottomUpReconciliator(target_level="region_level", source_level="city_level"),
)
bottom_up_metrics, _, _ = pipeline.backtest(ts=hierarchical_ts, metrics=[SMAPE()], n_folds=3, aggregate_metrics=True)
bottom_up_metrics = bottom_up_metrics.set_index("segment").add_suffix("_bottom_up")
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.3s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.7s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 1.0s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 1.0s finished
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.4s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.7s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 1.0s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 1.0s finished
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.1s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s finished
3.2. Top-down approach#
Top-down approach is based on the idea of generating forecasts for time series at higher hierarchy levels and then performing disaggregation to lower levels. This approach can be expressed with the following formula:
In matrix notations this equation could be rewritten as:
The main challenge of this approach is proportions estimation. In ETNA library, there are two methods available:
Average historical proportions (AHP)
Proportions of the historical averages (PHA)
Average historical proportions
This method is based on averaging historical proportions:
where \(n\) - window size, \(T\) - latest timestamp, \(y_{i, t}\) - time series at the lower level, \(y_t\) - time series at the higher level. Both \(y_{i, t}\) and \(y_t\) have hierarchical relationship.
Proportions of the historical averages This approach uses a proportion of the averages for estimation:
where \(n\) - window size, \(T\) - latest timestamp, \(y_{i, t}\) - time series at the lower level, \(y_t\) - time series at the higher level. Both \(y_{i, t}\) and \(y_t\) have hierarchical relationship.
Described methods require only series at the higher level for forecasting. Advantages of this approach are: simplicity and reliability. Loss of information is main disadvantage of the approach.
This method can be useful when it is needed to forecast lower level series, but some of them have more noise. Aggregation to a higher level and reconciliation back helps to use more meaningful information while modeling.
[26]:
from etna.reconciliation import TopDownReconciliator
TopDownReconciliator accepts four arguments in its constructor. You need to specify reconciliation levels, a method and a window size. First, let’s look at the AHP top-down reconciliation method.
[27]:
ahp_reconciliator = TopDownReconciliator(
target_level="region_level", source_level="reason_level", method="AHP", period=6
)
The top-down approach has slightly different dataset levels requirements in comparison to the bottom-up method. Here source level should be higher than the target level, and the current dataset level should not be higher than the target level.
After all level requirements met and the reconciliator is fitted, we can obtain the mapping matrix. Note, that now mapping matrix contains reconciliation proportions, and not only zeros and ones.
Columns of the top-down mapping matrix correspond to segments at the source level of the hierarchy, and rows to the segments at the target level.
[28]:
ahp_reconciliator.fit(ts=hierarchical_ts)
ahp_reconciliator.mapping_matrix.toarray()
[28]:
array([[0.29517217, 0. , 0. , 0. ],
[0.17522331, 0. , 0. , 0. ],
[0.29906179, 0. , 0. , 0. ],
[0.06509802, 0. , 0. , 0. ],
[0.10138424, 0. , 0. , 0. ],
[0.0348691 , 0. , 0. , 0. ],
[0.02919136, 0. , 0. , 0. ],
[0. , 0.35663824, 0. , 0. ],
[0. , 0.19596791, 0. , 0. ],
[0. , 0.25065754, 0. , 0. ],
[0. , 0.06313639, 0. , 0. ],
[0. , 0.09261382, 0. , 0. ],
[0. , 0.02383924, 0. , 0. ],
[0. , 0.01714686, 0. , 0. ],
[0. , 0. , 0.29766462, 0. ],
[0. , 0. , 0.16667059, 0. ],
[0. , 0. , 0.27550314, 0. ],
[0. , 0. , 0.0654707 , 0. ],
[0. , 0. , 0.13979554, 0. ],
[0. , 0. , 0.0245672 , 0. ],
[0. , 0. , 0.03032821, 0. ],
[0. , 0. , 0. , 0.29191277],
[0. , 0. , 0. , 0.15036933],
[0. , 0. , 0. , 0.25667986],
[0. , 0. , 0. , 0.09445469],
[0. , 0. , 0. , 0.1319362 ],
[0. , 0. , 0. , 0.03209989],
[0. , 0. , 0. , 0.04254726]])
Let’s fit HierarchicalPipeline with AHP method.
[29]:
reconciliator = TopDownReconciliator(target_level="region_level", source_level="reason_level", method="AHP", period=9)
pipeline = HierarchicalPipeline(
transforms=[
LagTransform(in_column="target", lags=[1, 2, 3, 4, 6, 12]),
],
model=LinearPerSegmentModel(),
reconciliator=reconciliator,
)
ahp_metrics, _, _ = pipeline.backtest(ts=hierarchical_ts, metrics=[SMAPE()], n_folds=3, aggregate_metrics=True)
ahp_metrics = ahp_metrics.set_index("segment").add_suffix("_ahp")
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.3s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.4s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.4s finished
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.1s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s finished
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.1s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s finished
To use another top-down proportion estimation method pass different method name to the TopDownReconciliator constructor. Let’s take a look at the PHA method.
[30]:
pha_reconciliator = TopDownReconciliator(
target_level="region_level", source_level="reason_level", method="PHA", period=6
)
It should be noted that the fitted mapping matrix has the same structure as in the previous method, but with slightly different non-zero values.
[31]:
pha_reconciliator.fit(ts=hierarchical_ts)
pha_reconciliator.mapping_matrix.toarray()
[31]:
array([[0.29761574, 0. , 0. , 0. ],
[0.17910202, 0. , 0. , 0. ],
[0.29400697, 0. , 0. , 0. ],
[0.0651224 , 0. , 0. , 0. ],
[0.10000206, 0. , 0. , 0. ],
[0.03596948, 0. , 0. , 0. ],
[0.02818132, 0. , 0. , 0. ],
[0. , 0.35710317, 0. , 0. ],
[0. , 0.19744442, 0. , 0. ],
[0. , 0.24879185, 0. , 0. ],
[0. , 0.06362301, 0. , 0. ],
[0. , 0.09206311, 0. , 0. ],
[0. , 0.02404128, 0. , 0. ],
[0. , 0.01693316, 0. , 0. ],
[0. , 0. , 0.29730368, 0. ],
[0. , 0. , 0.16779538, 0. ],
[0. , 0. , 0.27544335, 0. ],
[0. , 0. , 0.06506127, 0. ],
[0. , 0. , 0.139399 , 0. ],
[0. , 0. , 0.02441176, 0. ],
[0. , 0. , 0.03058557, 0. ],
[0. , 0. , 0. , 0.28940705],
[0. , 0. , 0. , 0.14772684],
[0. , 0. , 0. , 0.26106345],
[0. , 0. , 0. , 0.09481879],
[0. , 0. , 0. , 0.13193001],
[0. , 0. , 0. , 0.03034655],
[0. , 0. , 0. , 0.04470731]])
Let’s fit HierarchicalPipeline with PHA method.
[32]:
reconciliator = TopDownReconciliator(target_level="region_level", source_level="reason_level", method="PHA", period=9)
pipeline = HierarchicalPipeline(
transforms=[
LagTransform(in_column="target", lags=[1, 2, 3, 4, 6, 12]),
],
model=LinearPerSegmentModel(),
reconciliator=reconciliator,
)
pha_metrics, _, _ = pipeline.backtest(ts=hierarchical_ts, metrics=[SMAPE()], n_folds=3, aggregate_metrics=True)
pha_metrics = pha_metrics.set_index("segment").add_suffix("_pha")
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.1s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s finished
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.1s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s finished
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.1s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.3s finished
Finally, let’s forecast the middle level series directly.
[33]:
region_level_ts = hierarchical_ts.get_level_dataset(target_level="region_level")
pipeline = Pipeline(
transforms=[
LagTransform(in_column="target", lags=[1, 2, 3, 4, 6, 12]),
],
model=LinearPerSegmentModel(),
)
region_level_metric, _, _ = pipeline.backtest(ts=region_level_ts, metrics=[SMAPE()], n_folds=3, aggregate_metrics=True)
region_level_metric = region_level_metric.set_index("segment").add_suffix("_region_level")
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.3s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.5s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.5s finished
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.4s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.6s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.6s finished
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.1s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.2s finished
Now we can take a look at metrics and compare methods.
[34]:
all_metrics = pd.concat([bottom_up_metrics, ahp_metrics, pha_metrics, region_level_metric], axis=1)
all_metrics
[34]:
| SMAPE_bottom_up | SMAPE_ahp | SMAPE_pha | SMAPE_region_level | |
|---|---|---|---|---|
| segment | ||||
| Bus_NSW | 5.270422 | 5.015657 | 4.814298 | 7.059593 |
| Bus_NT | 25.765018 | 16.629957 | 16.210839 | 12.718326 |
| Bus_QLD | 18.254162 | 3.653159 | 3.769619 | 16.946310 |
| Bus_SA | 15.282322 | 16.694209 | 16.940077 | 16.967729 |
| Bus_TAS | 30.695013 | 27.307973 | 26.523334 | 24.133560 |
| Bus_VIC | 15.116212 | 4.571119 | 4.359536 | 14.334224 |
| Bus_WA | 10.009304 | 17.026675 | 16.926661 | 13.688767 |
| Hol_NSW | 14.454165 | 12.399630 | 11.994909 | 17.043741 |
| Hol_NT | 53.250687 | 44.744583 | 49.765493 | 55.005842 |
| Hol_QLD | 9.624166 | 11.851425 | 13.983468 | 9.840566 |
| Hol_SA | 8.202269 | 29.610151 | 29.559022 | 9.343553 |
| Hol_TAS | 51.592386 | 45.207863 | 45.832426 | 48.459946 |
| Hol_VIC | 7.125269 | 17.840854 | 16.883132 | 7.421170 |
| Hol_WA | 16.415138 | 23.793483 | 25.208175 | 18.636453 |
| Oth_NSW | 29.987238 | 34.912603 | 34.685216 | 23.790318 |
| Oth_NT | 98.032493 | 49.537936 | 54.553245 | 94.936352 |
| Oth_QLD | 31.464303 | 25.776690 | 26.905804 | 33.150413 |
| Oth_SA | 24.098806 | 31.959505 | 32.030506 | 28.638613 |
| Oth_TAS | 55.187208 | 36.601269 | 34.369745 | 37.551688 |
| Oth_VIC | 31.365795 | 29.007615 | 26.359892 | 34.186411 |
| Oth_WA | 26.894592 | 22.888604 | 25.102690 | 24.231688 |
| VFR_NSW | 4.977585 | 10.066277 | 10.065904 | 4.568697 |
| VFR_NT | 46.565888 | 23.537350 | 23.650015 | 40.369501 |
| VFR_QLD | 12.675037 | 13.975730 | 14.587780 | 4.299708 |
| VFR_SA | 15.613376 | 16.390740 | 15.695589 | 5.758916 |
| VFR_TAS | 33.182773 | 25.492236 | 25.177505 | 33.747570 |
| VFR_VIC | 9.237164 | 17.037192 | 16.725030 | 12.894987 |
| VFR_WA | 17.416115 | 15.014164 | 15.509316 | 14.953232 |
[35]:
all_metrics.mean()
[35]:
SMAPE_bottom_up 25.634104
SMAPE_ahp 22.448023
SMAPE_pha 22.792472
SMAPE_region_level 23.738495
dtype: float64
The results presented above show that using reconciliation methods can improve forecasting quality for some segments.
4. Exogenous variables for hierarchical forecasts#
This section shows how exogenous variables can be added to a hierarchical TSDataset.
Before adding exogenous variables to the dataset, we should decide at which level we should place them. Model fitting and initial forecasting in the HierarchicalPipeline are made at the source level. So exogenous variables should be at the source level as well.
Let’s try to add monthly indicators to our model.
[36]:
from etna.datasets.utils import duplicate_data
horizon = 3
exog_index = pd.date_range("2006-01-01", periods=periods + horizon, freq="MS")
months_df = pd.DataFrame({"timestamp": exog_index.values, "month": exog_index.month.astype("category")})
reason_level_segments = hierarchical_ts.hierarchical_structure.get_level_segments(level_name="reason_level")
[37]:
months_ts = duplicate_data(df=months_df, segments=reason_level_segments)
months_ts.head()
[37]:
| segment | Bus | Hol | Oth | VFR |
|---|---|---|---|---|
| feature | month | month | month | month |
| timestamp | ||||
| 2006-01-01 | 1 | 1 | 1 | 1 |
| 2006-02-01 | 2 | 2 | 2 | 2 |
| 2006-03-01 | 3 | 3 | 3 | 3 |
| 2006-04-01 | 4 | 4 | 4 | 4 |
| 2006-05-01 | 5 | 5 | 5 | 5 |
Previous block showed how to create exogenous variables and convert to a hierarchical format manually. Another way to convert exogenous variables to a hierarchical dataset is to use TSDataset.to_hierarchical_dataset.
First, let’s convert the dataframe to hierarchical long format.
[38]:
months_ts = duplicate_data(df=months_df, segments=reason_level_segments, format="long")
months_ts.rename(columns={"segment": "reason"}, inplace=True)
months_ts.head()
[38]:
| timestamp | month | reason | |
|---|---|---|---|
| 0 | 2006-01-01 | 1 | Hol |
| 1 | 2006-02-01 | 2 | Hol |
| 2 | 2006-03-01 | 3 | Hol |
| 3 | 2006-04-01 | 4 | Hol |
| 4 | 2006-05-01 | 5 | Hol |
Now we are ready to use to_hierarchical_dataset method. When using this method with exogenous data pass return_hierarchy=False, because we want to use hierarchical structure from target variables. Setting keep_level_columns=True will add level columns to the result dataframe.
[39]:
months_ts, _ = TSDataset.to_hierarchical_dataset(df=months_ts, level_columns=["reason"], return_hierarchy=False)
months_ts.head()
[39]:
| segment | Bus | Hol | Oth | VFR |
|---|---|---|---|---|
| feature | month | month | month | month |
| timestamp | ||||
| 2006-01-01 | 1 | 1 | 1 | 1 |
| 2006-02-01 | 2 | 2 | 2 | 2 |
| 2006-03-01 | 3 | 3 | 3 | 3 |
| 2006-04-01 | 4 | 4 | 4 | 4 |
| 2006-05-01 | 5 | 5 | 5 | 5 |
When dataframe with exogenous variables is prepared, create new hierarchical dataset with exogenous variables.
[40]:
hierarchical_ts_w_exog = TSDataset(
df=hierarchical_df,
df_exog=months_ts,
hierarchical_structure=hierarchical_structure,
freq="MS",
known_future="all",
)
[41]:
f"df_level={hierarchical_ts_w_exog.current_df_level}, df_exog_level={hierarchical_ts_w_exog.current_df_exog_level}"
[41]:
'df_level=city_level, df_exog_level=reason_level'
Here we can see different levels for the dataframes inside the dataset. In such case exogenous variables wouldn’t be merged to target variables.
[42]:
hierarchical_ts_w_exog.head()
[42]:
| segment | Bus_NSW_city | Bus_NSW_noncity | Bus_NT_city | Bus_NT_noncity | Bus_QLD_city | Bus_QLD_noncity | Bus_SA_city | Bus_SA_noncity | Bus_TAS_city | Bus_TAS_noncity | Bus_VIC_city | Bus_VIC_noncity | Bus_WA_city | Bus_WA_noncity | Hol_NSW_city | Hol_NSW_noncity | Hol_NT_city | Hol_NT_noncity | Hol_QLD_city | Hol_QLD_noncity | Hol_SA_city | Hol_SA_noncity | Hol_TAS_city | Hol_TAS_noncity | Hol_VIC_city | Hol_VIC_noncity | Hol_WA_city | Hol_WA_noncity | Oth_NSW_city | Oth_NSW_noncity | Oth_NT_city | Oth_NT_noncity | Oth_QLD_city | Oth_QLD_noncity | Oth_SA_city | Oth_SA_noncity | Oth_TAS_city | Oth_TAS_noncity | Oth_VIC_city | Oth_VIC_noncity | Oth_WA_city | Oth_WA_noncity | VFR_NSW_city | VFR_NSW_noncity | VFR_NT_city | VFR_NT_noncity | VFR_QLD_city | VFR_QLD_noncity | VFR_SA_city | VFR_SA_noncity | VFR_TAS_city | VFR_TAS_noncity | VFR_VIC_city | VFR_VIC_noncity | VFR_WA_city | VFR_WA_noncity |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| feature | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target | target |
| timestamp | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2006-01-01 | 1201 | 1684 | 136 | 80 | 1111 | 982 | 388 | 456 | 116 | 107 | 1164 | 984 | 532 | 874 | 3096 | 14493 | 101 | 86 | 4688 | 4390 | 888 | 2201 | 619 | 1483 | 2531 | 7881 | 1383 | 2066 | 396 | 510 | 35 | 8 | 431 | 271 | 244 | 73 | 76 | 24 | 181 | 286 | 168 | 37 | 2709 | 6689 | 28 | 9 | 3003 | 2287 | 1324 | 869 | 602 | 748 | 2565 | 3428 | 1019 | 762 |
| 2006-02-01 | 2020 | 2281 | 138 | 170 | 776 | 1448 | 346 | 403 | 83 | 290 | 1014 | 811 | 356 | 1687 | 1479 | 9548 | 201 | 297 | 2320 | 3990 | 521 | 1414 | 409 | 689 | 1439 | 4586 | 1059 | 1395 | 657 | 581 | 69 | 39 | 669 | 170 | 142 | 221 | 36 | 61 | 229 | 323 | 170 | 99 | 2184 | 5645 | 168 | 349 | 1957 | 2945 | 806 | 639 | 257 | 266 | 1852 | 2255 | 750 | 603 |
| 2006-03-01 | 1975 | 2118 | 452 | 1084 | 1079 | 2300 | 390 | 360 | 196 | 107 | 1153 | 791 | 440 | 1120 | 1609 | 7301 | 619 | 745 | 4758 | 6975 | 476 | 1093 | 127 | 331 | 1488 | 3572 | 1101 | 2297 | 540 | 893 | 150 | 338 | 270 | 1164 | 397 | 315 | 32 | 23 | 128 | 318 | 380 | 1166 | 2225 | 5052 | 390 | 84 | 2619 | 2870 | 1078 | 375 | 130 | 261 | 1882 | 1929 | 953 | 734 |
| 2006-04-01 | 1500 | 1963 | 243 | 160 | 1128 | 1752 | 255 | 635 | 70 | 228 | 1245 | 508 | 539 | 1252 | 1520 | 9138 | 164 | 250 | 3328 | 4781 | 571 | 1699 | 371 | 949 | 1906 | 3575 | 1128 | 2433 | 745 | 1157 | 172 | 453 | 214 | 535 | 194 | 260 | 48 | 43 | 270 | 336 | 410 | 1139 | 2918 | 5385 | 244 | 218 | 2097 | 2344 | 568 | 641 | 137 | 257 | 2208 | 2882 | 999 | 715 |
| 2006-05-01 | 1196 | 2151 | 194 | 189 | 1192 | 1559 | 386 | 280 | 130 | 205 | 950 | 572 | 582 | 441 | 1958 | 14194 | 62 | 151 | 4930 | 5117 | 873 | 2150 | 523 | 1590 | 2517 | 8441 | 1560 | 2727 | 426 | 558 | 15 | 47 | 458 | 557 | 147 | 33 | 77 | 60 | 265 | 293 | 162 | 28 | 3154 | 7232 | 153 | 125 | 2703 | 2933 | 887 | 798 | 347 | 437 | 2988 | 3164 | 1396 | 630 |
Exogenous data will be merged only when both dataframes are at the same level, so we can perform reconciliation to do this. Right now, our dataset is lower, than the exogenous variables, so they aren’t merged. To perform aggregation to higher levels, we can use get_level_dataset method.
[43]:
hierarchical_ts_w_exog.get_level_dataset(target_level="reason_level").head()
[43]:
| segment | Bus | Hol | Oth | VFR | ||||
|---|---|---|---|---|---|---|---|---|
| feature | month | target | month | target | month | target | month | target |
| timestamp | ||||||||
| 2006-01-01 | 1 | 9815.0 | 1 | 45906.0 | 1 | 2740.0 | 1 | 26042.0 |
| 2006-02-01 | 2 | 11823.0 | 2 | 29347.0 | 2 | 3466.0 | 2 | 20676.0 |
| 2006-03-01 | 3 | 13565.0 | 3 | 32492.0 | 3 | 6114.0 | 3 | 20582.0 |
| 2006-04-01 | 4 | 11478.0 | 4 | 31813.0 | 4 | 5976.0 | 4 | 21613.0 |
| 2006-05-01 | 5 | 10027.0 | 5 | 46793.0 | 5 | 3126.0 | 5 | 26947.0 |
The modeling process stays the same as in the previous cases.
[44]:
region_level_ts_w_exog = hierarchical_ts_w_exog.get_level_dataset(target_level="region_level")
pipeline = HierarchicalPipeline(
transforms=[
OneHotEncoderTransform(in_column="month"),
LagTransform(in_column="target", lags=[1, 2, 3, 4, 6, 12]),
],
model=LinearPerSegmentModel(),
reconciliator=TopDownReconciliator(
target_level="region_level", source_level="reason_level", period=9, method="AHP"
),
)
metric, _, _ = pipeline.backtest(ts=region_level_ts_w_exog, metrics=[SMAPE()], n_folds=3, aggregate_metrics=True)
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.5s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.7s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.7s finished
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.4s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.6s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.6s finished
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.1s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.2s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 3 out of 3 | elapsed: 0.2s finished